| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Flyweight Pattern
- knapsack Problem
- 프로그래머스
- Modern C++
- Bronze
- 3D RPG
- level1
- Silver
- Zenject
- Euclidean
- two pointer
- dirtyflag pattern
- BFS
- level3
- Gold
- solid 원칙
- 프로세스 상태
- Unity
- trie
- 8-Puzzle
- binary search
- PrefixSum
- effective C++
- BOJ
- stack
- LEVEL2
- Project
- programmers
- algorithm
- SWEA
- Today
- Total
Patrick's Devlog
[Algorithm] Knapsack Problem 본문
개요
알고리즘 문제를 풀다가 배낭 관련 문제를 풀기 위해 기본적인 이론을 공부하고 코딩을 진행해보려고 한다. 저번처럼 유튜브 채널 코드없는 프로그래밍님의 Knapsack Problem 영상을 통해 공부를 진행할 예정이다. 자세한 내용을 알고싶다면 https://www.youtube.com/watch?v=rhda6lR5kyQ에서 확인하면 된다.
Knapsack Problem
배낭 문제는 Dynamic Programming의 아주 대표적인 문제이다. 이는 조합 최적화의 문제이다. 간단하게 설명하자면 한 여행가가 지니고 있는 배낭에 담을 수 있는 무게의 최댓값이 정해져 있으며, 일정 가치와 무게가 있는 짐들을 배낭에 넣을 때 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.

이해가 잘 안된다면 아래의 예시를 확인해보자.
먼저 가방의 최대 무게는 5Kg이다. 여기서 물건들의 값어치와 무게가 정해져서 아래의 표와같이 정리되어 있다.
| A | B | C | D | |
| value | 30 | 20 | 40 | 10 |
| weight | 1 | 2 | 3 | 4 |
이때, 이 가방에 넣을 수 있는 최대 value는 몇인지 구하는 것이다. 여러 방법을 통해서 최대 값을 구할 수 있다
1. Brute Force
각 물건이 들어있는지, 안들어있는지 계산하여 최댓값을 구하는 경우이다. 총 경우의 수는 2의 n제곱으로 확인할 수 있다. 너무 많은 시간이 낭비되므로, 선호되지 않는 방법이다.
2. Dynamic Programming
DP를 적용하면 problem과 sub-problem으로 나뉘게 될 것이다. 즉, Knapsack Problem에 A,B,C,D와 무게 제한 5를 나누는 방법을 생각하면 된다. 처음 접하면 Problem을 지정하기 힘들다. 특히나, 아래처럼 잘못 지정하면 안된다.
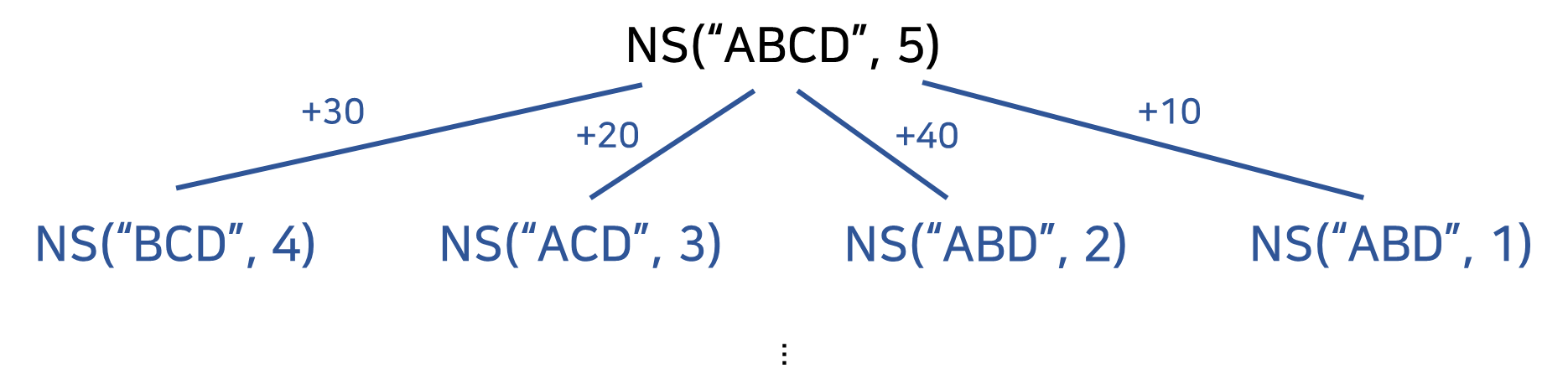
위의 방법처럼 sub-problem을 나눈 후에 max를 구하면 된다는 생각은 매우 잘못된 방법이다. 우리가 풀어야될 문제는 A,B,C,D 물건이 각각의 있는 경우와 없는 경우를 나누어야 한다는 것이다. 위의 sub-problem에서 problem으로 이동할 때 빠진 물건이 무조건 들어가게 되는 케이스로 나누고 있다. 즉, 위의 방식은 각각의 물건이 없을 경우가 정의되어 있지 않다.
다시 정확하게 정의를 해보자. 우리가 확인해야 할 부분은 배낭안에 물건이 있는지 없는지 생각을 해야한다.

위의 설명을 점화식으로 나타내면 아래의 식과 같다.
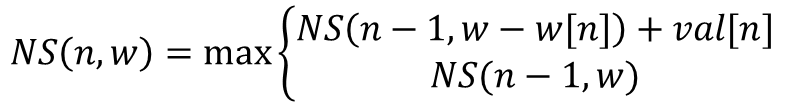
위의 공식을 이용해서 DP sub-problem의 solution을 저장하는 공간을 만들어보자. 위의 공식을 보면 변수가 n과 w가 존재한다. n은 몇가지의 물건이 있는지 변수로 나타낸 것이며, w는 현재 상태의 무게 limit이다. 이는 2차원의 테이블을 생성해야 한다는 의미이다.
| n \ w | 0 | 1 | 2 | 3 | 4 | 5 |
| (0) - | 0 | 0 | 0 | 0 | 0 | 0 |
| (1) A | 0 | 30 | 30 | 30 | 30 | 30 |
| (2) AB | 0 | 30 | 30 | 50 | 50 | 50 |
| (3) ABC | 0 | 30 | 30 | 50 | 70 | 70 |
| (4) ABCD | 0 | 30 | 30 | 50 | 70 | 70 |
좌측 (0)인 부분은 가방에 물건이 없을때이며, 각 알파벳은 물건이 존재할 때를 나타낸다. 이 표를 하나씩 채워나가면 최댓값을 구할 수 있다. 여기서 오른쪽 맨 하단의 숫자가 최종값임을 알 수 있다.
'Algorithm > Algorithms & Data Structure' 카테고리의 다른 글
| [Algorithm] Greedy (0) | 2022.10.27 |
|---|---|
| [Algorithm] 백트래킹(Backtracking) (0) | 2022.10.25 |
| [Algorithm] DFS/BFS (0) | 2022.07.12 |
| [Algorithm] 이진 탐색 (0) | 2022.06.29 |
| [Algorithm] Dynamic Programming (0) | 2022.05.13 |




