| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Bronze
- BOJ
- Silver
- SWEA
- Euclidean
- solid 원칙
- Unity
- level3
- Modern C++
- 프로그래머스
- 3D RPG
- Flyweight Pattern
- trie
- two pointer
- 8-Puzzle
- Gold
- Zenject
- BFS
- knapsack Problem
- stack
- level1
- binary search
- algorithm
- LEVEL2
- Project
- dirtyflag pattern
- 프로세스 상태
- programmers
- effective C++
- PrefixSum
- Today
- Total
Patrick's Devlog
[Algorithm] Dijkstra Algorithm(다익스트라 알고리즘) 본문
[Algorithm] Dijkstra Algorithm(다익스트라 알고리즘)
Patrick_ 2022. 11. 8. 16:211. Dijkstra Algorithm
음의 가중치가 없는 그래프의 한 정점(Vertex)에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘이다. 처음 알고리즘의 시간복잡조는 O(V^2)이나, 우선순위 큐 등을 이용해 더욱 개선된 알고리즘이 나오면서 최종적으로 O((V+E)logV)의 시간복잡도를 가지게 되었다. 여기서 V는 정점의 개수, E는 한 정점의 주변 노드이다.
그래프 방향 유무는 상관없으나, 간선(Edge)중 하나라도 가중치가 음수이면 알고리즘은 사용될 수 없다. 다익스트라를 확장시킨 알고리즘이 바로 A* 알고리즘이다.
1-1. Aigorithm
P[A][B] -> A와 B사이의 거리라고 가정
1. 출발점으로부터 최단거리를 저장할 배열 d[v] 생성, 출발 노드에는 0을 출발점을 제외한 다른노드들에는 매우큰 값 INF를 채워 넣음
2. 현재 노드를 나타내는 변수 A에 출발 노드 번호 저장
3. A로부터 갈 수 있는 임의의 노드 B에 대해, d[A] + P[A][B]와 d[B]의 값 비교
4. 만약 d[A] + P[A][B]의 값이 더 작다면, 짧은 경로임을 의미하고 d[B]의 값을 이 값으로 갱신
5. A의 모든 이웃 노드 B에 대해 이 작업 수행
6. A의 상태를 방문 완료로 바꿈 -> 더이상 A 사용 X
7. 미방문 상태인 모든 노드들 중, 출발점으로부터 거리가 제일 짧은 노드를 하나 골라 그 노드를 A에 저장
8. 도착 노드가 방문완료 상태거나, 혹은 더 이상 미방문 상태 노드를 선택할 수 없을때까지 3~7 과정 반복
이후 도착 노드에 저장된 값이 A로부터 최단거리이다. 만약 이 값이 INF 값이면, 중간에 길이 끊긴 것임을 의미한다.
1-2. Pseudo-code
function Dijkstra(graph, source):
dist[source] = 0; // 소스와 소스 사이 거리 초기화
prev[source] = undefined // 출발지 이전 최적 경로 추적은 없으므로 undefined
create vertex set Q // 노드들의 집합 Q 생성 시작
for each vertex v in graph: // graph 안에 있는 모든 노드 초기화
if v != source: // v노드가 출발지가 아닐 경우
dist[v] = INF // 소스와 v 노드 사이 알려지지 않은 거리
prev[v] = undefined // v노드 최적 경로 추적 초기화
add v to Q // graph에 존재하고 방금 전 초기화된 v 노드 Q에 추가
// graph에 존재하는 모든 노드들을 초기화 후 Q에 추가
while Q is not empty: // Q가 비어있지 않을 때 반복문 진행
u = vertex in Q with min dist[i] // 첫번째 반복에서는 dist[source] = 0이 선택
remove u from Q // u 노드를 방문한 것이므로 Q 집합에서 제거
for each neighbor v of u: // u 이웃 노드들과 거리 측정
alt = dist[u] + length(u, v) // 출발지 노드부터 계산된 u노드 까지 거리 + v에서 u의 이웃 노드까지 거리
if alt < dist[v]: // 방금 v노드까지 계산한 거리가 이전 v 노드까지 계산된 거리보다 가까운 경우
dist[v] = alt // v에 기록된 소스부터 v까지 최단 거리를 방금 v노드까지 계산한 거리로 변경
prev[v] = u // 제일 가까운 노드는 지금 방문하고 있는 노드로 변경
return dist[], prev[] // 계산된 거리값과 목적지 리턴1-3. 세부 설명
우선 A의 목표는 F까지 최단 거리 계산이며, 각 데이터의 의미는 다음과 같다
- S : 방문한 노드들 집합
- d[N] : A->N까지 계산된 최단거리
- Q : 방문하지 않은 노드들 집합
1. 다익스트라 알고리즘은 아직 확인되지 않은 거리는 전부 초기값을 무한으로 잡음

출발지를 A로 초기화 했으므로, d[A]는 0을 가진다. 출발지를 제외한 모든 노드는 방문하지 않았으므로, 무한값으로 지정했다(구현할 때 엄청 큰 값으로 지정해도 됨) Q는 아직 방문하지 않은 노드들의 집합이므로, 초기화 시 모든 노드들이의 집합이 된다. S는 공집합 상태이다
2. 루프를 돌려 이웃 노드 방문하고 거리 계산
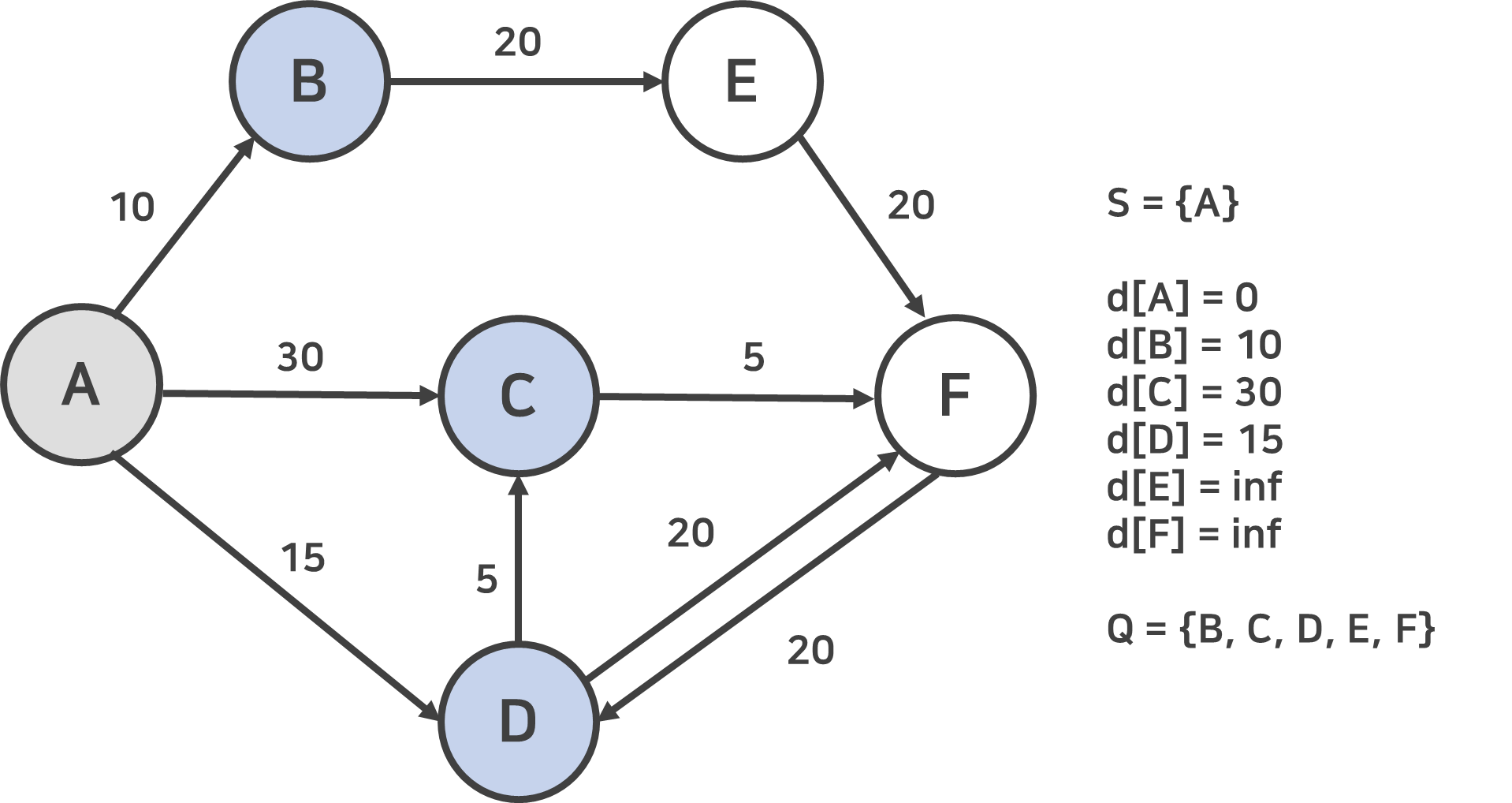
루프 시작은 거리가 최소인 노드를 Q에서 제거한 후 그 노드를 S에 추가한다. 즉, N을 방문한다는 의미이다. 이후, 모든 이웃 노드와의 거리를 측정해 (d[N] + N과 이웃노드간 거리값 = 출발지부터 이웃노드까지 거리값)이 계산된다. 지금은 첫번째 루프만을 끝난 상태이므로 단순히 (0 + 이웃노드와 출발사이의 거리값 = 출발지와 이웃노드 간의 거리값)이 이웃노드에 기록된다. 따라서 위의 숫자처럼 값을 변경한다.
3. 첫 루프 이후 그래프 상태가 업데이트 되는 방식
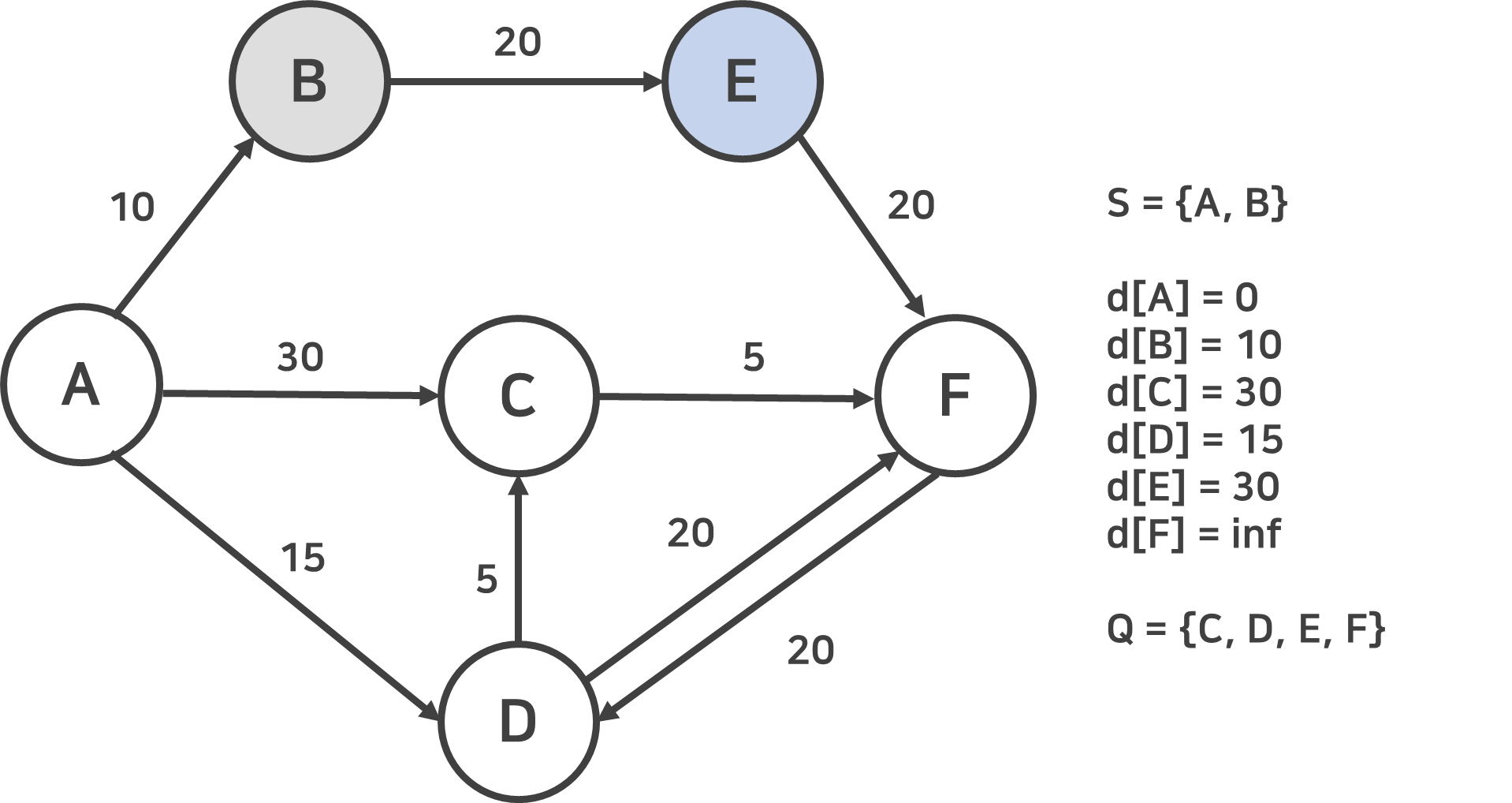
이제 루프가 반복적으로 작동할 것이다. 밑 그림들 또한 루프안에 알고리즘이 진행되는 순간들을 반복 설명한다. 방문할 노드는 Q에 남아있는 노드 중 d[N] 값이 제일 작은것으로 선택된다. 따라서 d[B] = 10으로 제일 작은 값이므로, B를 방문하여 S에 추가하고 Q에 제거한다. 이제 B의 이웃 노드들을 모두 탐색하고 거리를 재어 d[N]에 기록한다. B의 이웃노드는 E뿐이므로, d[E]값이 무한에서 d[B] + 20 = 30으로 업데이트 된다.
4. 더 빠른 경로를 발견한 경우
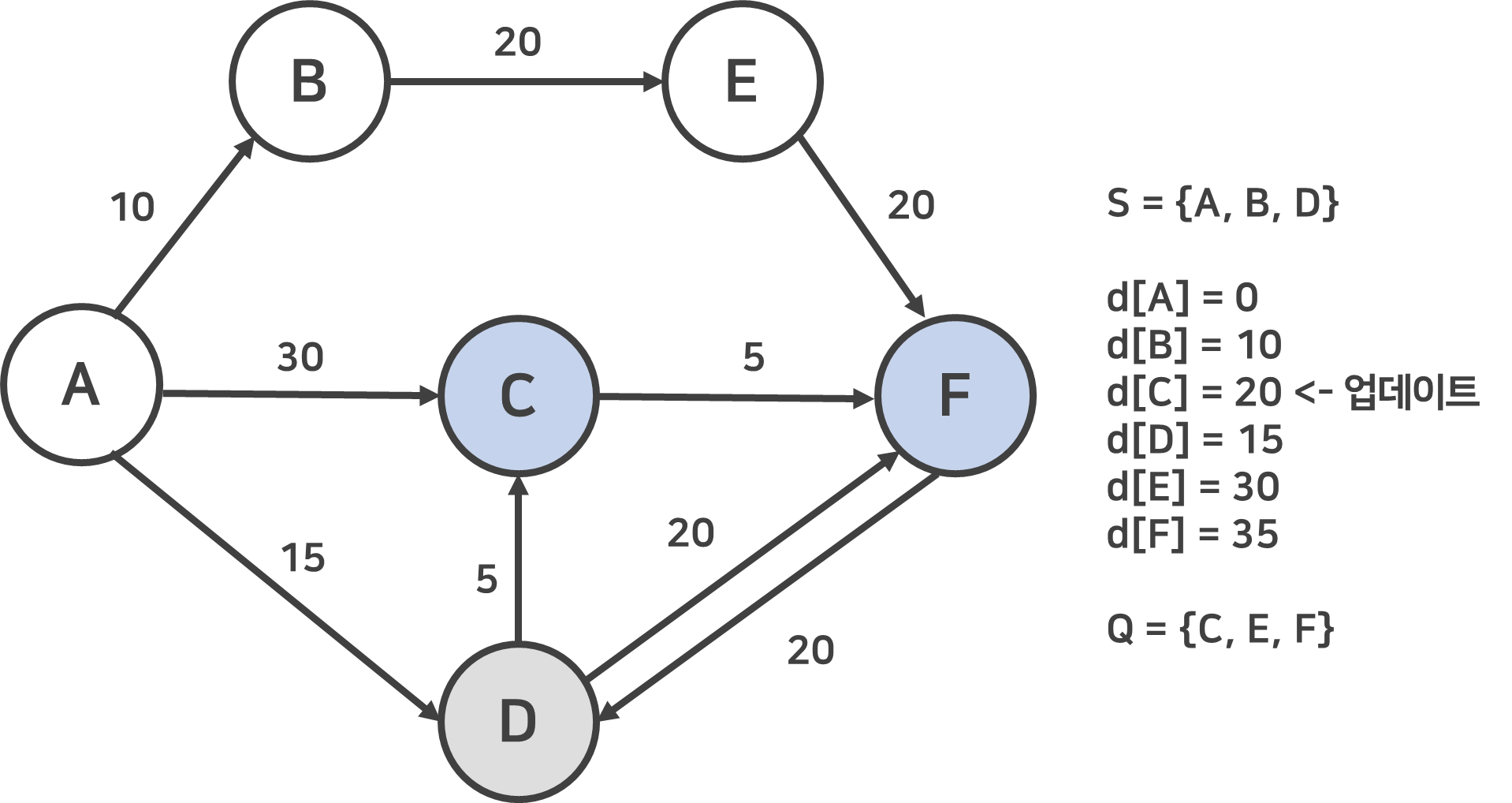
이번에 선택되는 노드는 D이다. Q 원소 중, 제일 낮은 d[N]값을 가지고 있기 때문이다. 따라서 Q에서는 제외해주고 S에 추가되었다. 이제 D의 이웃 노드들 (C, F)의 거리를 잰 후 d[N]값을 업데이트 한다. 여기서 주의깊게 봐야할 점은 d[C]의 값이 이미 30으로 계산되었으나, D를 방문해 C와의 거리를 확인해보니 20으로 더 짧은 최단 경로가 발견되었다. 그러므로 d[C]는 20으로 변경해주어야 한다.
5. 또 다른 반복 루프 상황
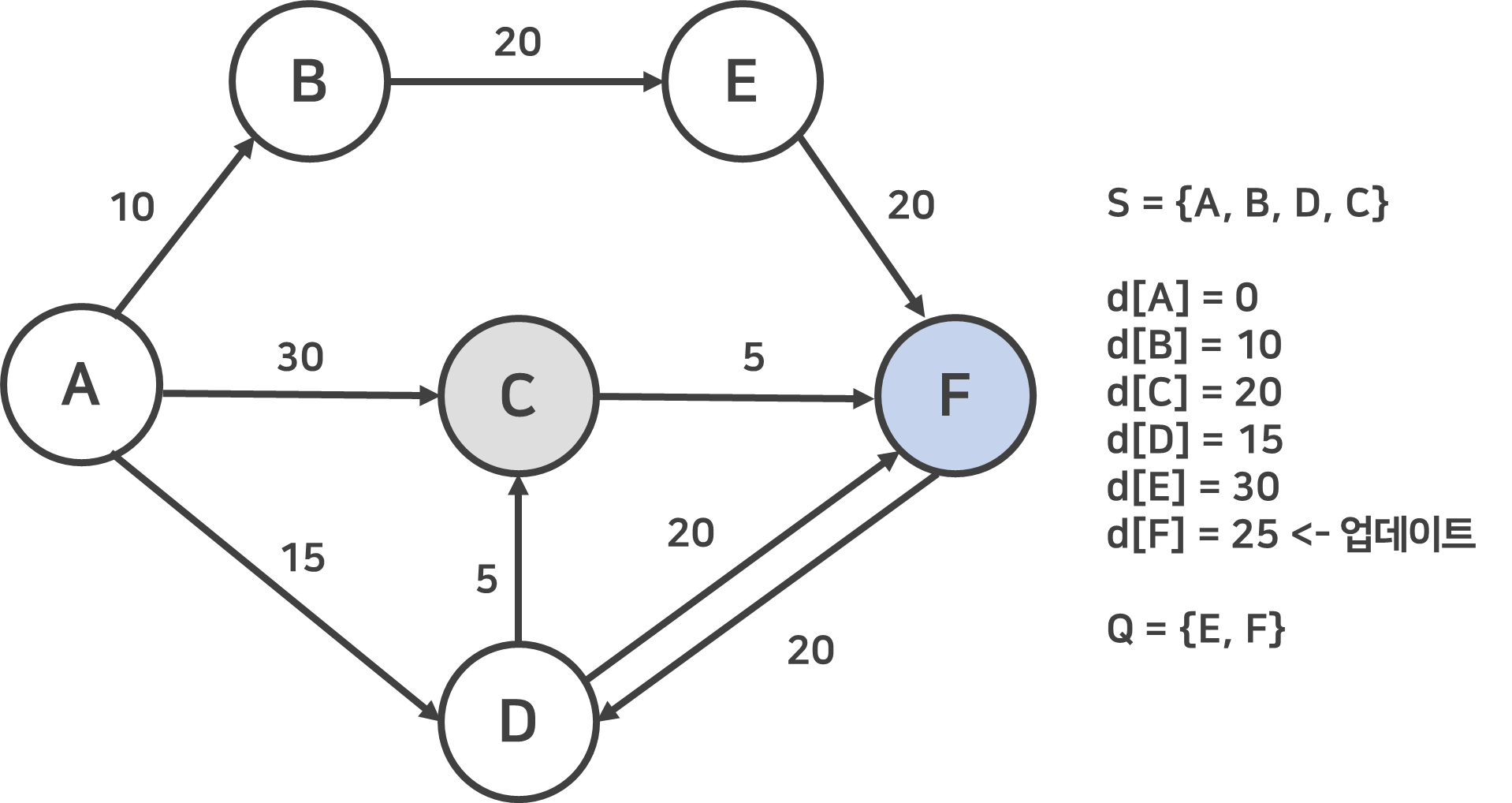
Q에서 d[C]가 20이므로 C를 방문해 S는 C가 추가된다. 다시 계산해보면, 기존 35였던 d[F]가 A->D->C->F를 계산해보면 25로 더 작은 값을 가지는 것이 발견되었다.
마지막 루프 이후,
s = {A, B, D, C, F, E}
d[A] = 0
d[B] = 10
d[C] = 20
d[D] = 15
d[E] = 30
d[F] = 25
Q = {}
라는 값이 나오게 되며, 최단 경로는 A->D->C->F이며, 거리는 25로 결정된다.
참고 문서
데이크스트라 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 컴퓨터 과학에서 데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의
ko.wikipedia.org
다익스트라 알고리즘 - 나무위키
다익스트라 알고리즘은 다음과 같다. (P[A][B]는 A와 B 사이의 거리라고 가정한다) 출발점으로부터의 최단거리를 저장할 배열 d[v]를 만들고, 출발 노드에는 0을, 출발점을 제외한 다른 노드들에는
namu.wiki
'Algorithm > Algorithms & Data Structure' 카테고리의 다른 글
| [Algorithm] 유클리드 알고리즘 (0) | 2023.01.08 |
|---|---|
| [Algorithm] 투 포인터 알고리즘(Two Pointer Algorithm) (1) | 2022.11.22 |
| [Algorithm] Greedy (0) | 2022.10.27 |
| [Algorithm] 백트래킹(Backtracking) (0) | 2022.10.25 |
| [Algorithm] DFS/BFS (0) | 2022.07.12 |


